A new trivial proof of Bertrand’s Postulate
Create a graph defined on all $(x,y)$ pairs for $x,y\in\mathbb Z$ as follows:
- $(x,y)$ is a coordinate pair referring to one vertex/node, all of which are laid out in a grid graph.
- Every vertex $(x,y)$ has an edge leading either north (up, $+y$) or west (left, $-x$).
- If $\gcd(x,y)=1$, that is, $x$ is coprime to $y$, the edge connects $(x,y)$ to $(x-1,y)$.
- If $\gcd(x,y)>1$, that is, $x$ shares a factor with $y$, the edge connects $(x,y)$ to $(x,y+1)$.
- The value of vertex $(x,y)$ will be $\gcd(x,y)$.
Here’s what you end up with:
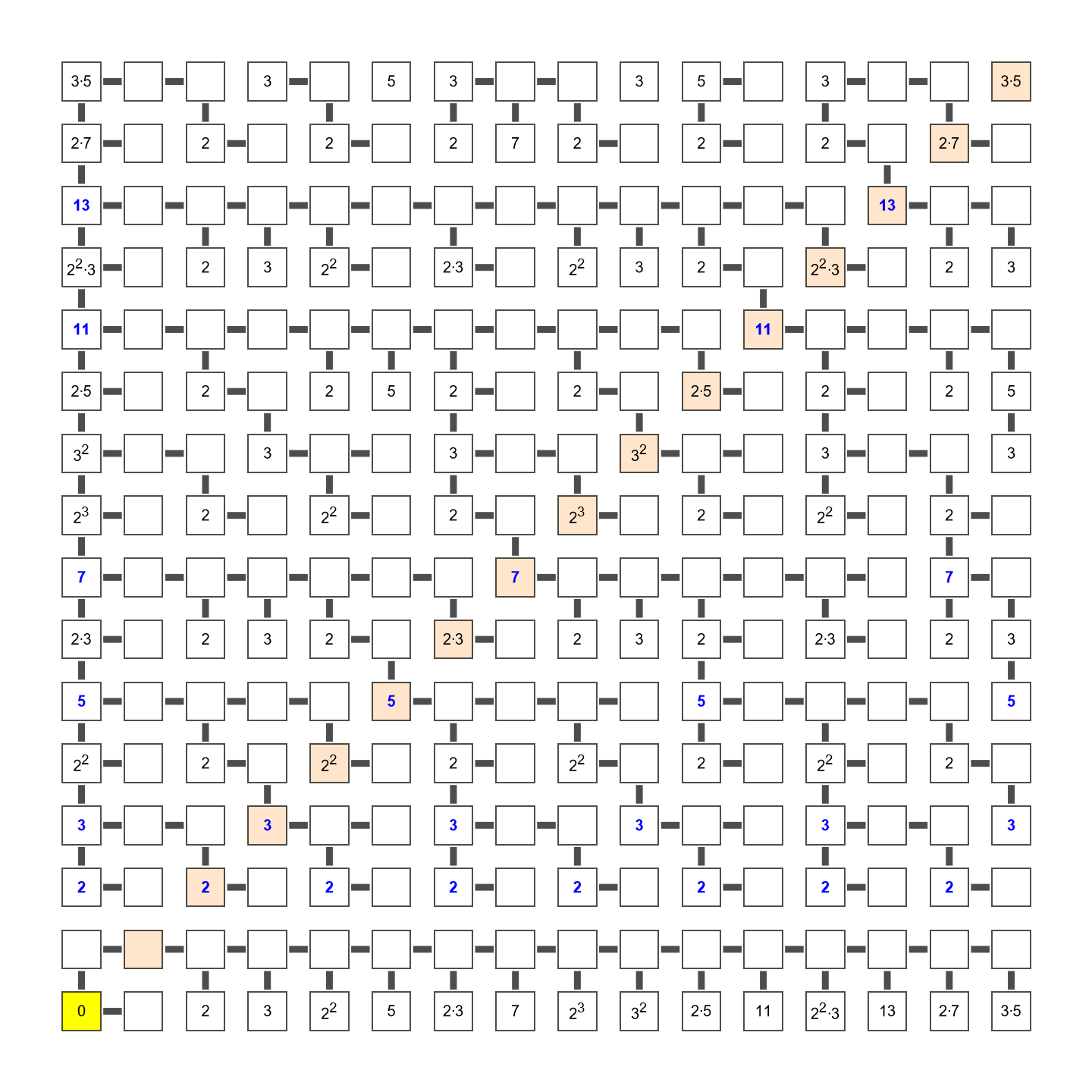
An identical graph could be created by starting at $(0,0)$ and printing out $\mathbb{N}$
using coordinate steps of $(m,n)$ where $m,n \in\mathbb Z$ and $\gcd(m,n)=1$.
E.g. offsets of $(1,2)$ and $(2,1)$ make knight moves, counting out $1,2,3,\dots$ as they go.
This graph has a number of useful properties for our purposes:
Since every vertex has an edge leading north or west, you can start at any vertex and trace an infinite edge path heading somewhere between north and west, inclusive. Note this is not true in the other direction: edge paths heading south/east all terminate at some point.
If two adjacent vertices on the same row do not have an edge connecting them, then any SE paths they have will also never connect; they can never meet. This is not true of NW paths, which can and do merge often.
Assertion 1
Let $(x,y)$ be any vertex that has an edge path heading south/east, and reaches the bottommost accessible row (we ignore the last two rows). Then that path must pass through vertices containing every prime smaller than $y$, in descending order (along with other interposing values).
Proof
For any prime-numbered row $p$, the only vertices reachable from above will occur at $(kp,p)$ for all $k\in\mathbb Z$. Moving south one row always implies you’re moving onto a vertex with $\gcd(x,y)>1$, as otherwise there would be no vertical edge to use, and $\gcd(kp,p)=p$ is the only non-$1$ value there can be on any row $p$. Since any edge path that travels unbroken from above a row to some point below it obviously passes through it, that also means the path passes through a vertex with value $p$ on row $p$, for all prime rows.
This works even better in reverse. In particular, since we can start at any vertex and be guaranteed an infinite path to the north/west, this means that any such path starting at some $(x,y)$ must pass through prime-valued vertices for all primes larger than $y$. Again, on prime rows, the prime-valued vertices function as choke points when heading in either direction.
So all $p_i$-valued vertices $(kp_i,p_i)$ will have a path north/west which reaches every row above $p_i$. But we’ll just consider the next prime-valued vertex/row, $(rp_{i+1},p_{i+1})$. This shows that there will always be a path from every prime-valued vertex on row $p_i$ to a prime-valued vertex on row $p_{i+1}$.
E.g. every $5$ on row $5$ will have a distinct NW path leading through one $7$ vertex on row $7$, one $11$ vertex on row $11$, and so forth. Note that in the opposite direction, a prime may have more than one path, each one leading to a different vertex, as with the $5$ splitting to reach two $3$s.
Let $p$ be any prime, and consider the NW path starting at $(2p,p)$.
Since $\gcd(2p,p)=p$, its edge goes north, thus $(2p-1,p)$ and points west are unreachable.
Similarly, since every $\gcd(n,n-1)=1$ for any $n$, there cannot be an edge heading north from $(2p,2p-1)$.
This means that the path originating from $(2p,p)$ is constrained such that it must pass through exactly one point of the diagonal interval from $(p,p)$ to $(2p,2p)$, exclusive. Since that point must be coprime to every prime smaller than $p$, it must be a prime larger than $p$. Specifically, it must be the next larger prime after $p$, since if there were another one in between, it would have intercepted the path instead.
If your path goes to the bottom, as it must since we’re coming from $(2p,p)$, you encounter all primes $p$ and smaller. This could not happen if one of those factors divided $(n,n)$, since you would be unable to reach that factor in your path.
Assertion 2
If $(n,n)$ has a connected SE path of length $p$ to prime $p$, where $p<n$, then $p$ and $n$ are coprime.
Proof
If it takes $p$ edge steps moving south or east to reach a vertex with value $p$, what is that really saying?
The Manhattan distance between $(n,n)$ and your destination $p$ vertex is $p$. Let $a$ be the total steps to the east, your $x$-diff, and let $b$ be the steps to the south, your $y$-diff.
Then $a+b=p$. Also, $\gcd(n+a,n-b)=1$.
If $a+b=p$, then almost regardless of choice of $a,b$, we have $\gcd(a,b)=1$. The one exception to this is if $a=0$ and $b=p$ or vice versa. However, that maps to a configuration in which the prime $p$ is found at $(n+p,n)$ or $(n,n-p)$, respectively; for the same reasons explained in the last section, there can be no path from $(n,n)$ to either of them. This means $(n,n)$ would have no $p$-length path to that prime $p$, and it would also mean that $p \mid n$, i.e. that $\gcd(p,n)\geq p$.
There will be some legitimate situations where you cannot reach a given $p$ in $p$ steps. If there is a $1$ (i.e. empty) vertex at $(n+p,n)$, that is equivalent to having a path to $p$, meaning $\gcd(n,p)=1$.
