On the persistence of zeros in Rule 30
A tentative proof of the aperiodicity of the center column in Wolfram’s Rule 30 open question.
Outline
- Instead of assigning ones and zeros, we’ll be using boolean algebra to represent cell values. This allows us to ratchet up the complexity of the system in a slightly more general way. Let $k$ be the number of contiguous boolean variables we start out with; these variables are set on top of an infinitely long background of $0$ cells (per the problem definition). We refer to these variables as seed variables, and the top row as the seed row.
- We show that the distribution of those boolean expressions which appear infinitely many times in a column are well-behaved with regards to the distribution of seed variables.
- One of the effects of this regular distribution is the guarantee of null cells in every column.
- We show that the presence of such a null cell—that is, a cell containing only a $0$, indicating it cannot be impacted by seed variables—is sufficient to prevent center column cycling.
1. Computing Rule 30 as boolean expressions.
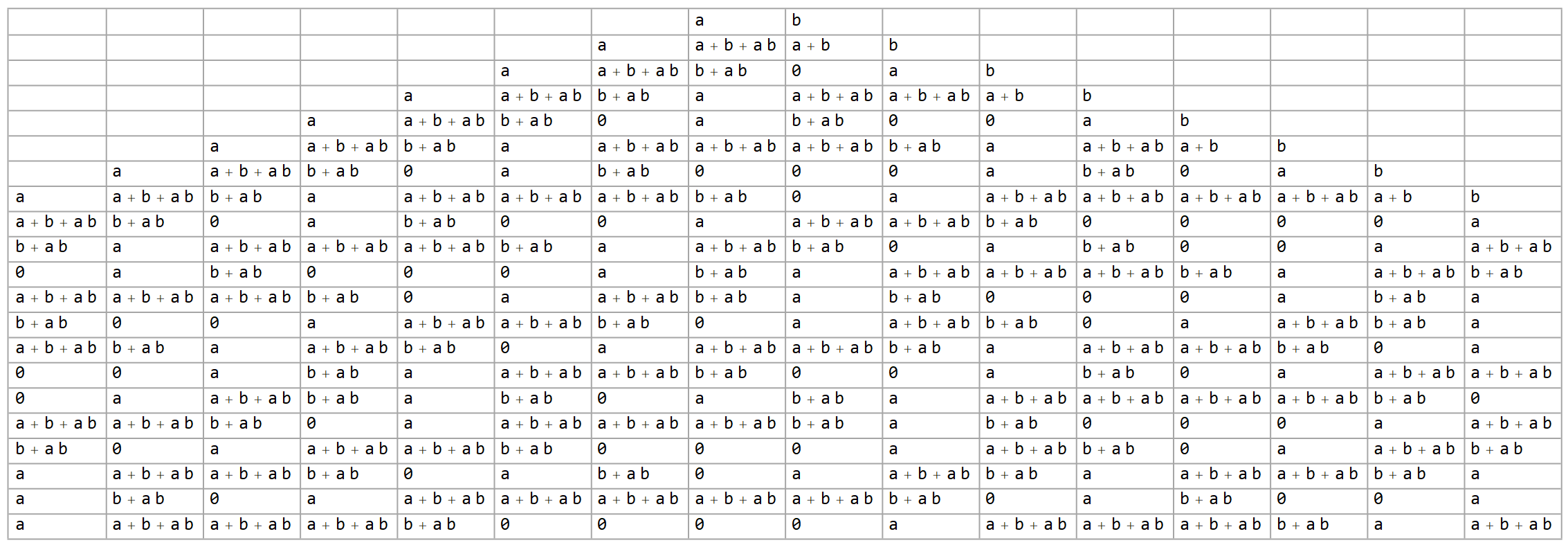
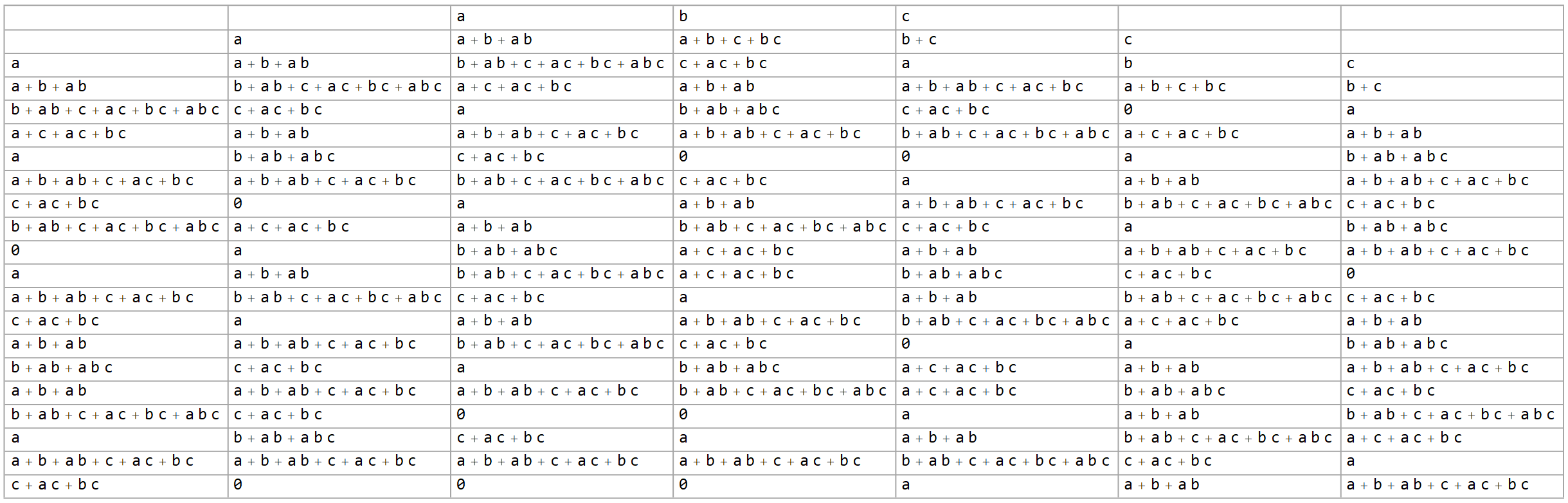
The principle is simple. Rather than starting with ones and zeros, we start with an arbitrary number of variables. All subsequent calculations are carried out in the same way. The principle operation of Rule 30 is $p \otimes (q \lor r)$, which we’ll be representing in boolean algebra as $f(a,b,c)=a+b+c+bc \pmod 2$.
To give some concept of this, see the three examples below, representing 1-, 2- and 3-variable configurations respectively.
See my earlier post here for a slightly gentler approach to most of this if any of it is confusing.
Note that when carrying out the Rule 30 function in this context, we can do some simple optimizing simplification to keep things clean. Exponents can be dropped without effect, as $1^m=1$ and $0^m=0$. Terms with even coefficients can be dropped completely, as they’re modded out, and odd coefficients can be omitted, i.e. an implied $1$. This leaves you with tidy polynomials that are simply sums of products, having no constants other than the occasional $0$ when everything else cancels.
As you can see in the tables above, the 1-seed-variable version has a roughly equal number of $a$ and $0$ cells. Note that we could assign the value $1$ to $a$, and it immediately becomes a standard Rule 30 layout. (Note also that any empty cells contain $0$s as well, but are left blank for legibility.)
Moving on to the 2-variable version, I assert the expected frequency of a $0$-cell drops to $1/4$. Likewise, for the 3-variable version, it drops to $1/8$. Where it goes from there actually depends on interpretation.
2. Single-variable vs. extended polynomials
Using $a+b+c+bc$ as a naive formula explodes to intractability nearly instantaneously. We save quite a lot by employing the simplification shortcuts listed earlier, but even that’s not enough; the complexity of the full expressions, even simplified, grows doubly exponentially. Using $k$ seed variables and our simplified polynomial form, there are still $2^{2^k-1}$ possible distinct expressions that can be formed. Not all of them are used, but enough are so that we have to simplify yet again. For the record, I believe that the number of them squares every step after $k=3$, giving something along the lines of $8^{2^{k-3}}$ distinct recurring polynomials. (These polynomials are interesting in their own right; I believe each one may more or less encode the entire structure to that point.)

Instead, we’ll accept that we’re really only interested in the case where one and only one seed variable is switched on. With that assumption, any product in those polynomials must have a $0$ and can be ignored, and only the single-variable monomial terms are of interest to us. There are several viable ways to generate these expressions; the easiest turns out to be simply running Rule 30 as usual, reversing the bit order, and swapping in seed variables for $1$ bits.
Using that, the monster expression above becomes $a_1+a_5+a_8+a_9$. So yes, a tad easier to work with.
3. The utility of a null cell.
These are not to be confused with the more familiar $0$ you’d find in a cellular automaton; the $0$s we’re concerned with are boolean expressions, in particular empty ones, and thus are much more infrequent.
Once we have our algebraic interpretation laid out, we can manipulate things to some extent. If we assign a $1$ value to any single one of our seed variables, it will effectively horizontally translate the entire structure. If we want, we can even assign the values ordinarily corresponding to a later row, which has the effect of translating the structure vertically.
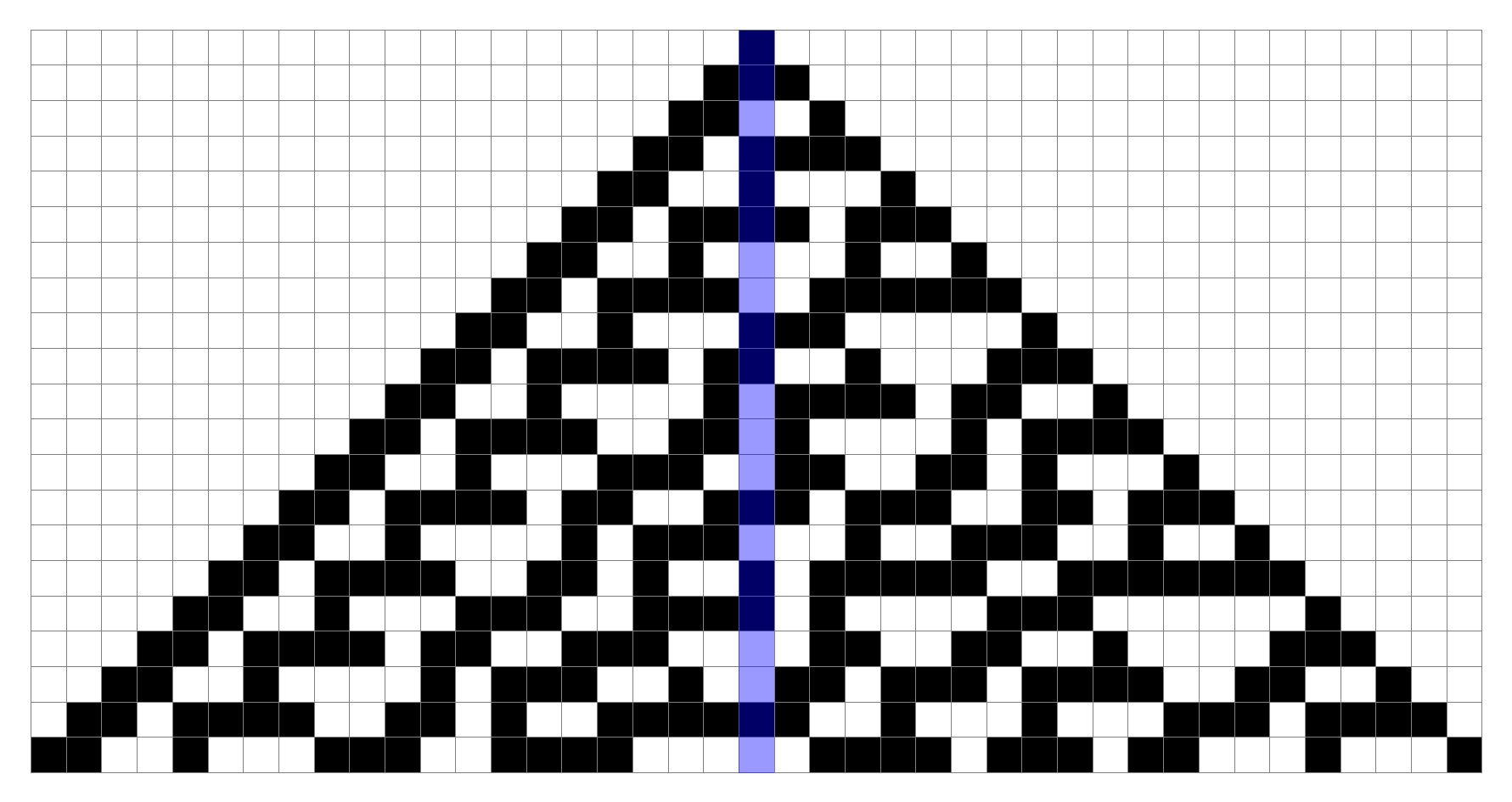
For our purposes, all we need to realize is that if we encounter a $0$-expression cell, it means that no possible setting of the current seed variables can toggle this bit. Consider that, within the bounds of our seed variable sequence, we could opt to place our initial $1$ seed cell all the way to the left, or way off to the right; yet, if a cell has only $0$ in it, clearly turning on any one bit just won’t be sufficient to light up that cell. In fact, it indicates that the corresponding $k$ cells in the row with the zero are all $0$-valued, in the typical sense of $0$. This in turn indicates a “white triangle” of width at least $k$, and implies a vertical run of $0$ cells of at least $k/2$, the height of the triangle.
Putting that all together, if we are able to start with an arbitrarily large $k$ and still be guaranteed to find a null expression eventually, that directly implies an arbitrarily large run of $0$ values in the center column. For any alleged period of length $p$, we need only set $k >2p$ and it shows such a cycle cannot exist.
Note that while I believe this proof is perfectly happy finding such null expressions in the center column itself, which is ideal if possible, it would also suffice to be able to reliably find one within any fixed constant distance from the center, provided we are still able to take an arbitrarily large $k$. Again, the important aspect is to expose a large enough run of zeros that it overshadows the center column and guarantees no cycle can survive the interruption.
4. Proof of existence.
This is the part I’d been stuck on since December. Everything up to this point is all well and good, and I am quite certain it’s all correct and provable. But how can we actually be sure we’ll see these null expressions? Their existence follows from virtually any heuristic or common sense approach you can take, yet they’ve been obnoxiously resistant to any real proof in that typical number-theoretic sort of way. Here goes nothing.
It’s readily apparent that any infinitely long column will repeat some number $m$ of distinct boolean expressions infinitely many times, given that there can only be finitely many such expressions under our constraints. In fact, since we’re only dealing with single-variable addends, the maximum number of distinct boolean expressions we can see in a cell, given $k$ seed variables, is $2^k$, the power set of those seed variables. For instance, $k=3$ means there will be at most $2^3=8$ different expressions, namely $\{0,a,b,c,a+b,a+c,b+c,a+b+c\}$.
However, those are possible expressions, and we have no guarantee we’ll see all of them. What we can say right off the bat is that the amount we’ll see must increase monotonically with $k$, as adding a fresh additional variable cannot possibly lessen the number of distinct expressions we have.
Moving on: there is some set $S$ of such expressions that will repeat infinitely many times for a given column. Ideally, we would like to show that $0$ is always in these sets, and as it turns out, there might be an easy way to do that. Since I prefer explanation through example, an example:
Suppose $k=3$, meaning I have the seed variables $a,b,c$ on my top row. Suppose that to this point, $0$ still appears in $S_x$ for all columns $x$.
Let’s increment to $k=4$, adding $d$ to our top row. It’s not hard to show that every seed variable appears in every row and every column at least once. Given that, we know that one or more of our expressions in $S$ now contain $d$. There are two primary cases we need to consider:
- $d \in S$.
- $d \not\in S$.
In the first case, we have an element in $S$ which is exactly $d$, meaning the expression $d$ appears by itself in a cell infinitely many times in this column. Since any new seed variable yields new expressions in a strictly additive way, every new term in $S$ will be a logical-OR in the form $X+d$, where $X \in S$ is some pre-existing expression. For a variable like $d$ to appear on its own requires that prior to its inclusion, we have $0 \in S$, as only $0+d=d$. Thus case 1 affirms the presence of a $0$ in $S$.
There is arguably a case to be made that that most recent seed variable was somehow perfectly arranged to hit every remaining $0$ cell in that column, effectively removing it from $S$, but this is handled by the second case. Suppose that $d$ replaced all remaining $0$ cells; if so, proceed to add another seed variable, and continue with the following argument.
In the second case, there is no single $d$ added to $S$. This means that either no null cell remains, or through some dark magic, the zeros and the $d$’s never overlap.
In either case, we’re still guaranteed at least one expression containing a $d$. This one will necessarily have one or more other variables which would also trigger the cell, perhaps something like $b\lor c \lor d=b+c+d+bc+bd+cd+bcd=b+c+d$. Remember, since we are asserting only one seed variable may be turned on, we still omit products.
The issue now is that this expression, and any other multi-variable expressions, can be removed by unwinding our process using an alternate path. Suppose $S=\{a,b,c,a+b,b+c,a+d,b+c+d\}$, an impossible but illustrative example. Let’s remove seed variable $a$, something we’re perfectly allowed to do whenever we like; this has the effect of removing any element of $S$ referencing $a$, leaving $S=\{b,c,b+c,b+c+d\}$. Next we’ll remove $b$ (which we’ll assume was magically covering all $0$s for this example), leaving $S=\{0,c\}$, and finally we remove $c$, leaving $S=\{0\}$. If $0$ is our only potential expression in any column, it indicates that no seed variable can be turned on, as otherwise any variable would plow inexorably along the left and right diagonals, altering every row and column at some cell.
However, we never actually removed $d$ explicitly, meaning that by rights, we ought to be able to set it to $1$ and light everything up. This clear impossibility is our contradiction, and the implication is that any time we add a seed variable, it must be of Case 1 type, meaning it includes itself as an entire cell expression. And since that implies that a $0$ is present or was present on the previous step, and since we can carry this out multiple times, we may be assured that a $0$ is always in $S$, for any column, which is sufficient to prove that the center column never becomes periodic.